Craps Rolling Odds
Calculating craps odds and probability seems hard, but it's not as complicated as one might think. When calculating the probabilities of any gambling activity, the first thing one looks at is the number of potential outcomes. When rolling two six-sided dice, like you in a game of craps, there are 36 possible outcomes. An “odds bet” (i.e. “free odds bet”) is a type of craps bet (described in Part I) available to line bettors after the shooter establishes a point. The “odds in favor of” or the “odds against” an event are ways to measure how likely it is for that event to occur. The odds of actually rolling a 7 are 6 in 36 or 5:1. The house pays out 4:1 on a winning bet, which brings up an outrageous house edge of 16.67%. This is the absolute worst bet you can make in craps. There are 6 ways to roll a “7”. Some writers say there are three ways to roll a “7”: 1 and 6, 2 and 5, or 3 and 4. However, the math has to account for each die separately; hence, the probability of rolling a “7” in craps is 1 in 6. In declining order of probability, the possible combinations in craps are: 7 (1 in 6) 6 or 8 (5 in 36).
Chart on the possibility of each number being rolled.
When playing online Craps, it is important to understand the probability of each dice combination being rolled. Once you know what the probability is, you can work out what the house edge is on particular bets. The odds paid to you, the probability of your bet being successful and the house edge are all important factors in how lucrative Craps will be for you.
Why Use a Craps Probability Chart?
The more information that you have at our disposal, the better decisions you can make. A more informed and smarter Craps player has a much better chance of winning on a regular basis. Whether you are a seasoned online craps professional or a casual players, a craps probability chart is crucial to understanding the probability of each dice roll result. With this knowledge, you can make smarter bets at the craps table.
For example, you can see on our craps probability chart that the most common number to come up after a dice roll is a seven. This is the reason that most craps professionals will recommend the pass line as the smartest bet you can make when formulating a solid craps strategy. On the other hand, you can easily see that, according to our craps probability chart, the most uncommon dice roll results are two (or snake eyes in many circles) and 12. Taking this into account, making a bet on two or 12 would likely not be the best bet that you could make.
How to Use a Craps Probability Chart

Obviously, there is nothing to stop you from printing out our craps probability chart and posting it by your computer any time that you are playing craps online. However, by reading our extensive section on the rules and etiquette of craps in offline casinos, you will also find that there are no rules preventing you from printing out the craps probability chart (or copying it on paper with a pencil) and bringing it with you to your favorite offline craps casino.
Every time you are considering a bet, you can consult the craps probability chart to see if the odds match up to the amount of your bet. However, a craps probability chart is simply a tool and cannot alone formulate your entire craps strategy. Some situations require a great deal more information than a craps probability chart before determining whether or not the bet is wise. For more information, you can consult our craps strategy section if you are unsure how to discover the total odds of a bet being successful. For now, memorizing the craps probability chart is your first step towards becoming a craps professional.
The game of craps is a wonderful opportunity to enjoy an energetic casino experience. The high enthusiasm for the game is mixed with the lure of “tempting fate” with the chance of betting on dice rolls. Players and onlookers rejoice together when the shooter hits the point and satisfies several bets, or lament together when the “dice” are against them.
In addition to this, part of what craps offers interested gamblers is a simple way to work the odds of the casino to a player’s favor. Winning at craps is entirely about learning the true probabilities of certain dice rolls occurring and making sure a player has money on the rolls with the best probability. The surest way to win in craps is to maximize bets with good odds and avoid bets with very poor odds.
Dice Probability
The essential starting ground for craps odds and probabilities is with the dice roll itself. Since bets are made based on the potential outcome of the dice, knowing how often, or how infrequently a number combination will occur is the foundation for betting odds in craps.
A pair of standard six-sided dice offers thirty-six possible number combinations that can occur with each roll. First, players need to understand that craps, and dice probabilities are literally roll by roll. Mathematically, what makes craps a game of chance is that every time the shooter picks up the dice, the exact same overall odds apply. There are not cumulative effects roll by roll, so the gambler’s fallacy of “what hasn’t occurred in a while is more likely to occur soon” cannot apply to craps, though many players bet like it will.
In reality, the dice odds stack in a pyramid that symmetrically pairs combinations of numbers, which have the same odds of occurring. The most frequently rolled number is a seven, which a player can mathematically expect to see once in every six rolls. This high probability is due to the fact that seven has the highest possible number of dice combinations to form it between the two dice.
The craps dice odds and probabilities list as follows:
- 2 and 12 have only one way they can be formed on two dice, thus carrying odds of 35 to 1 (a one in thirty-six chance of being rolled).
- 3 and 11 have two possible formations, so the odds of these appearing are 17 to 1.
- 4 and 10 each have three potential combinations, improving the odds of showing either of these to 11 to 1.
- 5 and 9 have four possible formations each, thus holding odds of 8 to 1.
- 6 and 8 are the second most frequently rolled combinations, with five possible ways to see a six or eight on the dice. The odds of either are 6.2 to 1.
- 7 has six possible formations, the most possible and gives it 5 to 1 odds of showing.
These odds are calculated by taking the number of possible formations out of thirty-six, reducing it to it’s lowest denominator and placing it in odds terms. For example, the four has three ways of being formed on the dice, thus a 3 in 36 chance of occurring or, reduced a one in twelve chance of being rolled. In odds terms one in twelve becomes 11 to 1. Understanding and remembering the dice odds is the basis for effective betting in craps.
The chance factor comes in with the fact that even though these odds are mathematically true over dozens and hundreds of rolls, and can be trusted to show in these ratios over a larger sample, they won’t “perfectly” occur with human shooters. Thus a shooter who gains six rolls can sometimes roll all six without showing a seven. This is what brings the element of risk and excitement to craps betting.
Making Good Odds Bets
There are three groupings of bets that have the best odds and the lowest house edge that a craps player can come by. These are the bread and butter of a craps player’s existence, and the wisest and winningest craps players use these bets like clockwork to maximize their odds of taking home cash, not just laying it down on the table. These are the most commonly used bets, as well.
On the right bettor side are the pass bet and the come bet. Pass bets are made during the come out roll; come bets are made after the shooter has established the point. Both of these are sweeping bets that the shooter will roll seven or eleven or a point number before rolling craps, 2, 3 and 12, the low frequency numbers. Pass bets and come bets parallel each other. Both of these bets have true odds of 251 to 244. The house edge, or casino advantage on these bets is one of the lowest at 1.41 %, which means bettors placing pass or come bets have a very good chance of winning this bet.
The wrong bettor partners to the pass and come bets are the don’t pass and don’t come bets. These bets go against the shooter (and thus are sometimes disliked by players), betting that the shooter will hit craps before hitting his point or seven. The house edge on these wrong bets actually drops further to 1.36%, and the odds of these bets showing are 976 to 949.
Free Odds Bets
The free odds bets that go with these are even better from an odds standpoint. The best bets to make in craps, free odds bets multiply a pass or come bet (or a don’t pass or don’t come bet). The advantage of these is the house edge gets lowered to almost zero, meaning players have a good chance of winning these bets at their actual mathematical odds. The odds bets have to be made in conjunction with the main pass/come and don’t pass/don’t come bets. On the right bettor side for pass and come odds bets, making this bet is called “taking the odds.” On the wrong bettor side, odds bets with don’t pass and don’t come bets are called “laying the odds.”
The pass odds and come odds bets have actual odds 2 to 1 on four and ten, 3 to 2 on five and nine, and 6 to 5 on six or eight. The payout ratios for these odds bets match the odds ratios for each number. On the don’t pass/don’t come odds side, the true odds are 1 to 2 against four and ten, 2 to 3 against five and nine, and 5 to 6 against six and eight. Again, the payout ratio when one of these bets wins is the same as the odds of occurrence.
Place Bet Odds
The third category of bets that use the dice probabilities to a great advantage are the place bets on the box numbers at the top of the craps table. Essentially, a place bet makes the same assertion as the free odds bet, that the shooter will roll one of these numbers before a seven or craps. The advantage to place bets is they can be made independently and don’t require a pass line bet first. However, the disadvantage is they payout at poorer odds than the free odds bets.
Four of the six possible place bets have a low house edge, making them still some of the better bets to make as far as player advantage. Place bets on six and eight have the third lowest house edge at 1.52%, making them very profitable bets. The odds of winning on place six and place eight bets are 6 to 5 or 45.45%. Payouts are at 7 to 6 odds. For even dollar payouts, player should bet in increments of $6 on these place bets, preventing rounding down by the casino on paying winnings.
Place bets on five and nine are also still lower house edges than most bets on the table at 4%. Players have a 40% chance of winning or 3 to 2 odds, and they payout at 7 to 5 odds. Place these bets in multiples of $5 for even dollar payouts without rounding.
Place bets on four and ten are still decent bets, but the house edge starts to climb–it’s 6.67%. The odds of winning a place four/place ten bet are 33.33% but if it does win, the payout rate is 9 to 5. These bets should also be made in $5 increments for even payout amounts.
Another advantage to place bets is that when a place bet wins, the dealer pays the player’s winnings but leaves the original bet on the table effectively starting another place bet. The player doesn’t have to add money to the bet to continue it. Players can ask the dealer to “turn off” the standing place bet or remove it if they wish.
A few online casinos offer the wrong side version of place bets called place bets to lose. Live casino Star City in Sydney, Australia also allows place bets to lose. These bets flip the bet to lose when the shooter hits the number first, but win if the shooter rolls a seven before the number. The odds of winning these place bets go from 54.55% to 66.67%, rather than under 50% for their right side counterparts. Place to lose on six and eight pay out at 4 to 5; on five and nine they pay out at 5 to 8; and on four and ten they pay out at 5 to 11.
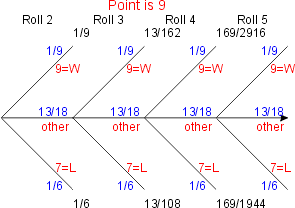
Craps Roll Odds
Betting the Field Odds
The field box bets are right in front of the players and can be enticing bets. Their major disadvantage stands in that they are single roll bets, only valid for the next immediate dice roll. The house edge at 5.56% is smaller than many other craps bets, but still starting to be larger than is wise for a player to use often. The payout odd for field bets on three, four, nine, ten and eleven are 1 to 1, even money. For the more rarely rolled two and twelve, the payout odds are 2 to 1. The true odds of betting on the field are 5 to 4.
Odds on Proposition Bets
The proposition bets located in the center of the craps table actually hold the poorest odds for a player, and with high house edges hold great odds for the casino winning. Craps experts consistently advise staying away from these various “sucker bets” that catch novices or people who have not bothered to learn a few key points about playing craps.
Proposition bets are mostly single, next roll bets on specific numbers. The rates of the occurrence for the dice roll is the first basis for the enticingly high payouts, but the house edge factors in on the lesser likelihood that the single next roll will produce that number or combination of numbers.

The list of odds for the main proposition bets is as follows:
- Craps 2 or 12 has true odds of 35 to 1, that single dice combination. The payout odds are 30 to 1, with a huge house edge of 13.89%.
- Single number bets on 3 or Yo (11) carry true odds of 17 to 1, but the casino pays 15 to 1 odds on a winning bet. The house edge is 11.11%
- A Hi-Lo bet matches the odds of 3/11 bets with true odds of 17 to 1 and payout odds of 15 to 1. The house edge is also 11.11%.
- Any Craps bets (looking for 2, 3, or 12) have true odds of 8 to 1, payouts of 7 to 1 and that ever-large 11.11% house edge.
- C-E or Craps-Eleven bets have true odds of 5 to 1. The payouts vary at 3 to 1 for craps (2, 3, 12) and 7 to 1 on eleven. This also carries an 11.11% house edge.
- Any 7 bets have true odds of 5 to 1 with payout odds at 4 to 1. Any 7 has the largest house edge on the table at 16.67%.
- Horn bets carry a higher house edge of 12.5%. The true odds are 5 to 1. Payout odds are 27 to 4 on two or twelve and 3 to 1 on three or eleven.
World or whirl bets are a variation of the horn bet on 2, 3, 7, 11 and 12. The true odds are 2 to 1. The payout odds on two or twelve are 26 to 5 and on three or eleven are 11 to 5. The house edge is 13.33%.
Big 6 and Big 8
The corner proposition bets of Big 6 and Big 8 have been banned from Atlantic City casino craps tables because the odds make them such poor bets. With a large house edge of 9.09%, bets on Big 6 and Big 8 only payout even money, though the true odds of rolling a six or eight before a seven, like in Place 6/Place 8 bets is 6 to 5.
Hardways Bets
Hardways proposition bets can be ongoing bets, but these are also costly bets to make. The hard four and hard ten bets have an 11.11% house edge and pay 7 to 1 if they win, but only carry an 11.11% chance of winning. Hard six and hard eight bets payout at 9 to 1, but only have a 9.09% chance of winning. The house edge for those two bets is 9.09%. It doesn’t seem like a bet bodes well for a player when the odds of winning equal the odds of the house advantage over the player.
Buy Bets and Lay Bets
For players who like to use place bets but who don’t like the odds, the option exists to buy the points for a 5% house commission that reduces the house advantage to “fair odds.” Some casinos require that commission up front; others take the commission on winnings. Most players will advise staying away from Buy and Lay bets. Paying extra to level the odds is simply not worth it. However, some players do like to use these bets.

Buy bets have a standard 4.76% house edge on all three pairs of bets. The odds are:
- Buy four and Buy ten have 2 to 1 odds.
- Buy five and Buy nine have 3 to 2 odds.
- Buy six and Buy eight have 6 to 5 odds.
Lay Bets are the “Place to Lose” or wrong side lay odds commission bets. The lay bet odds are slightly different than the buy bet odds.
- Lay four and Lay ten have 1 to 2 odds with a house edge of 2.44%.
- Lay five and Lay nine carry odds of 2 to 3 and a house edge of 3.23%.
- Lay six and Lay eight have 5 to 6 odds and a 4% house edge.
Overall Craps Odds
Some players ask about their overall chances of winning or losing at craps. Honestly, with most games of chance players will do well to expect to lose more than what they win. Statistically, in a particular session the mathematical odds reinforce the odds of losing are slightly greater than the odds of winning.
The odds of breaking even are about 0.67%.
For a truly big picture perspective on the odds of playing craps, probabilities calculated from simulating 1,000,000 sessions of 100 come out rolls each leave a players odds of winning and losing overall at the following percentages:
- Winning $1 to $25: probability 28.64%
Losing $1 to $25: probability 30.06% - Winning $26 to $50: probability 14.43%
Losing $26 to $50: probability 16.36% - Winning $51 to $75: probability 3.91%
Losing $51 to $75: probability 4.64% - Winning $76 to $100: probability 0.564%
Losing $76 to $100: probability 0.65% - Winning over $100: probability 0.0418%
Losing over $100: probability 0.0422%
With so many calculations for craps odds and probabilities, the best way for a player to utilize this information is to remember the dice probabilities and the most beneficial bets to use. Craps tables list the payout odds for the higher bets as part of inviting players to spend money on bets that the house is more likely to win than the player. Seeing a 30 to 1 payout option makes some folks eager to bet there for the big return, but the savvy player will remember that the odds of that single two or twelve showing up on the next roll are 35 to 1. There are many more useful places to invest those bets. Strong players will use these odds and probabilities on craps to make guided decisions about where best to bet their hard earned money.
Alter then so that one die has a six on every side, and the other one has all ones and fives.
Thanks for the kind words. No, I don't think that wishful thinking helps in the casino, all other things being equal.
The question on the dice influence is a hotly debated topic. Personally, I'm very skeptical. As I review this reply in 2013 I still have yet to see convincing evidence anybody can influence enough to have an advantage.
I'm very skeptical of it. I go over some of the experiments on the topic in my craps appendix 3.
I don’t believe in it. So far I have yet to see a name I respect endorse the method, nor any evidence that it works. While I don’t entirely rule out the possibility I am extremely skeptical of it. I may live in Nevada but when it comes to things like dice setting I’m from Missouri, 'show me' it works.
With ordinary dice, the like those you get in a board game, this is true. However casino dice have inlaid spots. At the factory they drill holes for the spots then insert white colored spots into the holes, of the same density as the die itself. So the die is essentially a perfect cube. Even if they did use ordinary dice from a board game I doubt the bias would be nearly enough to overcome the house edge.
I think there is no such thing as a naturally bad shooter. With the possible exception of a few pros all dice throws can be considered truly random. There are seminars on how to overcome the house edge in craps by precession throwing but I make no claims for or against them. I have yet to see enough evidence either way.
I lost the $1800 to another gambling writer, not Stanford. I would have preferred more rolls but there was an obvious time contraint. Assuming one throw per minute it would take 34.7 days to throw the dice 50,000 times. I wasn’t the one who decided on 500 but it seemed like a reasonable compromise between a large sample size and time. You are right that 500 is too few to make a good case for or against influencing the dice, but 500 throws is better than zero.
For large numbers of throws we can use the Gaussian Curve approximation. The expected number of sevens in 655 throws is 655 × (1/6) = 109.1667. The variance is 655 × (1/6) × (5/6) = 90.9722. The standard deviation is sqr(90.9722) = 9.5379. Your 78 sevens is 109.1667 − 78 = 31.1667 less than expectation. This is (31.1667 - 0.5)/9.5379 = 3.22 standard deviations below expectation. The probability of falling 3.22 or more standard deviations south of expectations is 0.000641, or 1 in 1,560. I got this figure in Excel, using the formula, normsdist(-3.22).
Craps Dice Roll Odds
This is about controlling the dice at Craps. You previously discussed the Stanford Wong Experiment, stating, 'The terms of the bet were whether precision shooters could roll fewer than 79.5 sevens in 500 rolls of the dice. The expected number in a random game would be 83.33. The probability of rolling 79 or fewer sevens in 500 random rolls is 32.66%.... The probability of rolling 74 or fewer sevens in 500 random rolls is 14.41%.'The question I have about this bet is that 14.41% still isn’t 'statistically significant' [ i.e. p < 0.05 ] , which is usually taken to mean greater than two Standard Deviations from the Mean -- or a probability of less than a *combined* 5% of the event happening randomly on EITHER end of the series.
How many Sevens would have to be rolled in 500 rolls before you could say that there is a less than 2.5% chance that the outcome was entirely random (i.e. that the outcome was statistically significant) ?
Many Thanks & BTW , yours is ABSOLUTELY the BEST web site on the subject of gambling odds & probabilities that I’ve found .... keep up the good work !!!
Thank you for the kind words. You should not state the probability that the throws were non-random is p. The way it should be phrased is the probability that a random game would produce such a result is p. Nobody expected 500 rolls to prove or disprove anything. It wasn’t I who set the line at 79.5 sevens, but I doubt it was chosen to be statistically significant; but rather, I suspect the it was a point at which both parties would agree to the bet.
The 2.5% level of significance is 1.96 standard deviations from expectations. This can be found with the formula =normsinv(0.025) in Excel. The standard deviation of 500 rolls is sqr(500*(1/6)*(5/6)) = 8.333. So 1.96 standard deviations is 1.96 * 8.333 = 16.333 rolls south of expectations. The expected number of sevens in 500 throws is 500*(1/6) = 83.333. So 1.96 standard deviations south of that is 83.333 − 16.333 = 67. Checking this using the binomial distribution, the exact probability of 67 or fewer sevens is 2.627%.
There is no definitive point at which confidence is earned. It is a matter of degree. First, I would ask what is being tested for, and what the shooter estimates will happen. With any test there are two possible errors. A skilled shooter might fail, because of bad luck, or a random shooter might pass because of good luck. Of the two, I would prefer to avoid a false positive. I think a reasonable test would set the probability of a false negative at about 5%, and a false positive at about 1%.
For example, suppose the claimant says he can average one total of seven every seven throws of the dice. A random shooter would throw one seven every six throws, on average. By trial and error I find that a test meeting both these criteria would be to throw the dice 3,600 times, and require 547 or fewer sevens to pass, or one seven per 6.58 rolls.
A one in seven shooter should average 514.3 sevens, with a standard deviation of 21.00. Using the Gaussian approximation, the probability of such a skilled shooter throwing 548 or more sevens (a false negative) is 5.7%. A random shooter should average 600 sevens, with a standard deviation of 22.36. The probability of a random shooter passing the test (a false positive) is 0.94%. The graph below shows the possibe results for skilled and random shooters. If the results are to the left of the green line, then I would consider the shooter to have passed the test, and I would bet on him.
The practical dilemma is if we assume two throws per minute, it would take 30 hours to conduct the test. Perhaps I could be more liberal about the significance level, to cut down the time requirement, but the results would not be as convincing. I do think the time has come for a bigger test than the 500-roll Wong experiment.
First of all, she rolled the dice a total of 154 times, with the 154th roll being a seven out (Source: NJ.com). However, that does not mean she never rolled a seven in the first 153 rolls. She could have rolled lots of them on come out rolls. As I show in my May 3, 2003 column, the probability of making it to the 154th roll is 1 in 5.6 billion. The odds of winning Mega Millions are 1 in combin(56,5)*46 = 175,711,536. So going 154 rolls or more is about 32 times as hard. Given enough time and tables, which I think exist, something like this was bound to happen sooner or later. So, I wouldn't suspect cheating. I roughly estimate the probability that this happens any given year to be about 1%.
Also see my solution, expressed in matrices, at mathproblems.info, problem 204.
I think some of the casinos in Las Vegas are using dice that are weighted on one side. As evidence, I submit the results of 244 throws I collected at a Strip casino. What are the odds results this skewed could come from fair dice?| Dice Test Data | |
| Dice Total | Observations |
| 2 | 6 |
| 3 | 12 |
| 4 | 14 |
| 5 | 18 |
| 6 | 23 |
| 7 | 50 |
| 8 | 36 |
| 9 | 37 |
| 10 | 27 |
| 11 | 14 |
| 12 | 7 |
| Total | 244 |
7.7%.
The chi-squared test is perfectly suited to this kind of question. To use the test, take (a-e)2/e for each category, where a is the actual outcome, and e is the expected outcome. For example, the expected number of rolls totaling 2 in 244 throws is 244×(1/36) = 6.777778. If you don’t understand why the probability of rolling a 2 is 1/36, then please read my page on dice probability basics. For the chi-squared value for a total of 2, a=6 and e=6.777778, so (a-e)2/e = (6-6.777778)2/6.777778 = 0.089253802.
Chi-Squared Results
| Dice Total | Observations | Expected | Chi-Squared |
| 2 | 6 | 6.777778 | 0.089253 |
| 3 | 12 | 13.555556 | 0.178506 |
| 4 | 14 | 20.333333 | 1.972678 |
| 5 | 18 | 27.111111 | 3.061931 |
| 6 | 23 | 33.888889 | 3.498725 |
| 7 | 50 | 40.666667 | 2.142077 |
| 8 | 36 | 33.888889 | 0.131512 |
| 9 | 37 | 27.111111 | 3.607013 |
| 10 | 27 | 20.333333 | 2.185792 |
| 11 | 14 | 13.555556 | 0.014572 |
| 12 | 7 | 6.777778 | 0.007286 |
| Total | 244 | 244 | 16.889344 |
Then take the sum of the chi-squared column. In this example, the sum is 16.889344. That is called the chi-squared statistic. The number of 'degrees of freedom' is one less than the number of categories in the data, in this case 11-1=10. Finally, either look up a chi-squared statistic of 10.52 and 10 degrees of freedom in a statistics table, or use the formula =chidist(16.889344,10) in Excel. Either will give you a result of 7.7%. That means that the probability fair dice would produce results this skewed or more is 7.7%. The bottom line is while these results are more skewed than would be expected, they are not skewed enough to raise any eyebrows. If you continue this test, I would suggest collecting the individual outcome of each die, rather than the sum. It should also be noted that the chi-squared test is not appropriate if the expected number of outcomes of a category is low. A minimum expectation of 5 is a figure commonly bandied about.
Whether or not it is called a valid roll depends on where you are. New Jersey gaming regulation 19:47-1.9(a) states:
A roll of the dice shall be invalid whenever either or both of the dice go off the table or whenever one die comes to rest on top of the other. -- NJ 19:47-1.9(a)
Pennsylvania has the exact same regulation, Section 537.9(a):
A roll of the dice shall be invalid whenever either or both of the dice go off the table or whenever one die comes to rest on top of the other. -- PA 537.9(a)
I asked a Las Vegas dice dealer who said that here it would be called a valid roll, if it was otherwise a proper throw. Although he has never seen it happen, he said if it did the dealers would simply move the top die to see what number the lower die landed on. However, one can determine the outcome of the lower die without touching, or looking through, the top die. Here is how to do it. First, by looking at the four sides you can narrow down the possibilities on top to two. Here is how to tell according to the three possibilities.
- 1 or 6: Look for the 3. If the high dot is bordering the 5, the 1 is on top. Otherwise, if it is bordering the the 2, the 6 is on top.
- 2 or 5: Look for the 3. If the high dot is bordering the 6, the 2 is on top. Otherwise, if it is bordering the the 1, the 5 is on top.
- 3 or 4: Look for the 2. If the high dot is bordering the 6, the 3 is on top. Otherwise, if it is bordering the the 1, the 4 is on top.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
This question was asked at TwoPlusTwo.com, and was answered correctly by BruceZ. The following solution is the same method as that of BruceZ, who deserves proper credit. It is a difficult answer, so pay attention.
First, consider the expected number of rolls to obtain a total of two. The probability of a two is 1/36, so it would take 36 rolls on average to get the first 2.
Next, consider the expected number of rolls to get both a two and three. We already know it will take 36 rolls, on average, to get the two. If the three is obtained while waiting for the two, then no additional rolls will be needed for the 3. However, if not, the dice will have to be rolled more to get the three.
The probability of a three is 1/18, so it would take on average 18 additional rolls to get the three, if the two came first. Given that there is 1 way to roll the two, and 2 ways to roll the three, the chances of the two being rolled first are 1/(1+2) = 1/3.
So, there is a 1/3 chance we'll need the extra 18 rolls to get the three. Thus, the expected number of rolls to get both a two and three are 36+(1/3)×18 = 42.
Next, consider how many more rolls you will need for a four as well. By the time you roll the two and three, if you didn't get a four yet, then you will have to roll the dice 12 more times, on average, to get one. This is because the probability of a four is 1/12.
What is the probability of getting the four before achieving the two and three? First, let's review a common rule of probability for when A and B are not mutually exclusive:
pr(A or B) = pr(A) + pr(B) - pr(A and B)
You subtract pr(A and B) because that contingency is double counted in pr(A) + pr(B). So,
pr(4 before 2 or 3) = pr(4 before 2) + pr(4 before 3) - pr(4 before 2 and 3) = (3/4)+(3/5)-(3/6) = 0.85.
The probability of not getting the four along the way to the two and three is 1.0 - 0.85 = 0.15. So, there is a 15% chance of needing the extra 12 rolls. Thus, the expected number of rolls to get a two, three, and four is 42 + 0.15*12 = 43.8.
Next, consider how many more rolls you will need for a five as well. By the time you roll the two to four, if you didn't get a five yet, then you will have to roll the dice 9 more times, on average, to get one, because the probability of a five is 4/36 = 1/9.
What is the probability of getting the five before achieving the two, three, or four? The general rule is:
pr (A or B or C) = pr(A) + pr(B) + pr(C) - pr(A and B) - pr(A and C) - pr(B and C) + pr(A and B and C)
So, pr(5 before 2 or 3 or 4) = pr(5 before 2)+pr(5 before 3)+pr(5 before 4)-pr(5 before 2 and 3)-pr(5 before 2 and 4)-pr(5 before 3 and 4)+pr(5 before 2, 3, and 4) = (4/5)+(4/6)+(4/7)-(4/7)-(4/8)-(4/9)+(4/10) = 83/90. The probability of not getting the four along the way to the two to four is 1 - 83/90 = 7/90. So, there is a 7.78% chance of needing the extra 7.2 rolls. Thus, the expected number of rolls to get a two, three, four, and five is 43.8 + (7/90)*9 = 44.5.
Continue with the same logic, for totals of six to twelve. The number of calculations required for finding the probability of getting the next number before it is needed as the last number roughly doubles each time. By the time you get to the twelve, you will have to do 1,023 calculations.
Here is the general rule for pr(A or B or C or ... or Z)
pr(A or B or C or ... or Z) =
pr(A) + pr(B) + ... + pr(Z)
- pr (A and B) - pr(A and C) - ... - pr(Y and Z) Subtract the probability of every combination of two events
+ pr (A and B and C) + pr(A and B and D) + ... + pr(X and Y and Z) Add the probability of every combination of three events
- pr (A and B and C and D) - pr(A and B and C and E) - ... - pr(W and X and Y and Z) Subtract the probability of every combination of four eventsThen keep repeating, remembering to add probability for odd number events and to subtract probabilities for an even number of events. This obviously gets tedious for large numbers of possible events, practically necessitating a spreadsheet or computer program.
The following table shows the the expected number for each step along the way. For example, 36 to get a two, 42 to get a two and three. The lower right cell shows the expected number of rolls to get all 11 totals is 61.217385.
Expected Number of Rolls Problem
| Highest Number Needed | Probability | Expected Rolls if Needed | Probability not Needed | Probability Needed | Expected Total Rolls |
|---|---|---|---|---|---|
| 2 | 0.027778 | 36.0 | 0.000000 | 1.000000 | 36.000000 |
| 3 | 0.055556 | 18.0 | 0.666667 | 0.333333 | 42.000000 |
| 4 | 0.083333 | 12.0 | 0.850000 | 0.150000 | 43.800000 |
| 5 | 0.111111 | 9.0 | 0.922222 | 0.077778 | 44.500000 |
| 6 | 0.138889 | 7.2 | 0.956044 | 0.043956 | 44.816484 |
| 7 | 0.166667 | 6.0 | 0.973646 | 0.026354 | 44.974607 |
| 8 | 0.138889 | 7.2 | 0.962994 | 0.037006 | 45.241049 |
| 9 | 0.111111 | 9.0 | 0.944827 | 0.055173 | 45.737607 |
| 10 | 0.083333 | 12.0 | 0.911570 | 0.088430 | 46.798765 |
| 11 | 0.055556 | 18.0 | 0.843824 | 0.156176 | 49.609939 |
| 12 | 0.027778 | 36.0 | 0.677571 | 0.322429 | 61.217385 |
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
The Wizard says that website sounds like a lot of ranting and raving with no credible evidence whatsoever to justify the accusation. I'd be happy to expose any casino for using biased dice, if I had any evidence of it.
If anybody has legitimate evidence of biased dice, I'd be happy to examine it and publish my conclusions. Evidence I would like to see are either log files of rolls or, better yet, some actual alleged biased dice.
Furthermore, if the casinos really were using dice that produced more than the expected number of sevens, then why aren't these detectives privy to the conspiracy out there betting the don't pass and laying the odds?
- 2 or 12: 1,000
- 3 or 11: 600
- 4 or 10: 400
- 5 or 9: 300
- 6 or 8: 200
My question is what is average bonus win?
Click the following button for the answer.
Click the following button for the solution.
Let x be the answer. As long as the player doesn't roll a seven he can always expect future wins to be x, in addition to all previous wins. In other words, there is a memory-less property to throwing dice in that no matter how many rolls you have already thrown you are no closer to a seven than you were when you started.Craps Roll Odds Table
I won't go into the basics of dice probabilities but just say the probability of each total is as follows:Craps Rolling Odds
- 2: 1/36
- 3: 2/36
- 4: 3/36
- 5: 4/36
- 6: 5/36
- 7: 6/36
- 8: 5/36
- 9: 4/36
- 10: 3/36
- 11: 2/36
- 12: 1/36
Before considering the consolation prize, the value of x can be expressed as:
x = (1/36)*(1000 + x) + (2/36)*(600 + x) + (3/36)*(400 + x) + (4/36)*(300 + x) + (5/36)*(200 + x) + (5/36)*(200 + x) + (4/36)*(300 + x) + (3/36)*(400 + x) + (2/36)*(600 + x) + (1/36)*(1000 + x)Next, multiply both sides by 36:
36x = (1000 + x) + 2*(600 + x) + 3*(400 + x) + 4*(300 + x) + 5*(200 + x) + 5*(200 + x) + 4*(300 + x) + 3*(400 + x) + 2*(600 + x) + (1000 + x)36x = 11,200 + 30x
6x = 11,200
x = 11,200/6 = 1866.67.
Next, the value of the consolation prize is 700*(6/36) = 116.67.
Thus, the average win of the bonus is 1866.67 + 116.67 = 1983.33.